On the use of Mahalanobis distance for out-of-distribution detection with neural networks for medical imaging

Harry Anthony & Konstantinos Kamnitsas

Defining the problem -
Out-of-distribution detection

When training a neural network, we have a set of training images and corresponding labels which we call the training data. We use this to train a neural network on a task of interest, such as classifying diseases from an x-ray scan. Once the model is trained, it can be applied to images without labels during inference. Most of these Images will be from the same distribution as the training data, known as in-distribution, however the model may encounter inputs which differ significantly from the training data, known as out-of-distribution.

Neural networks cannot be expected to give sensible predictions on OOD inputs, so we want to detect them to prevent erroneous predictions being used. This is a significant issue for AI in medical image analysis, as wrong predictions on OOD inputs could have serious implications for decisions made downstream.

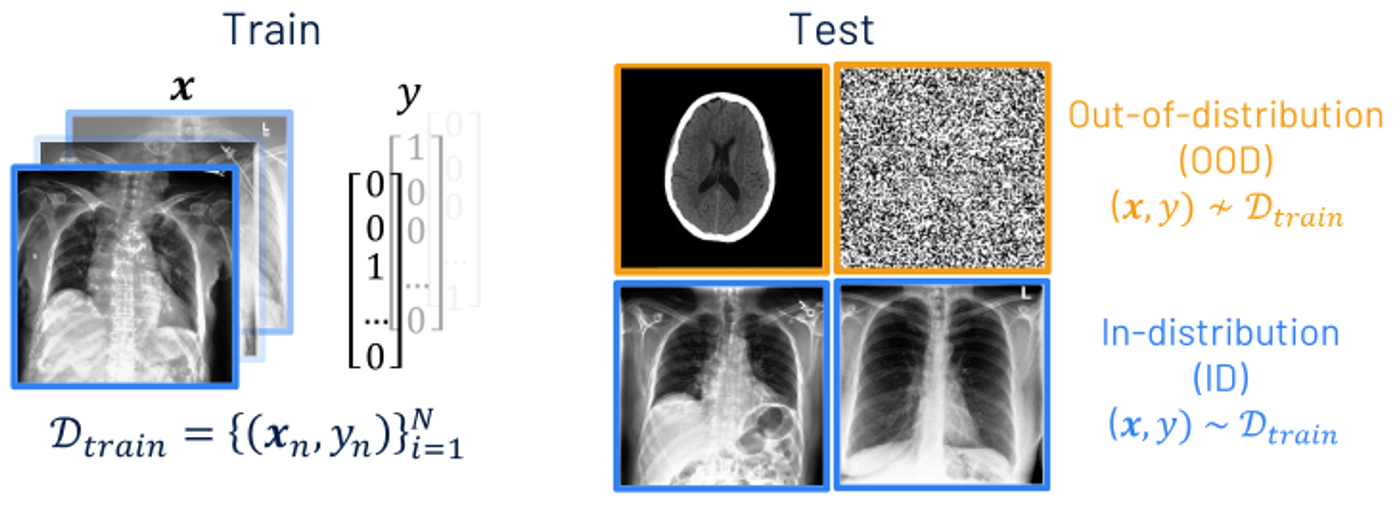
OOD detection can be viewed as a binary classification problem, labelling an input $\mathbf{x}$ as OOD when the scoring function $\mathcal{S}(\mathbf{x},f)$ is below a threshold $\lambda$, and ID if it is above. Such a scoring function should identify if the input is from a different distribution to $\mathcal{D}_{\text {train}}$.

$$ G_{\lambda}(\mathbf{x})= \begin{cases}\text { OOD } & \text { if } \mathcal{S}(\mathbf{x}) \leq \lambda \\ \text { ID } & \text { if } \mathcal{S}(\mathbf{x}) > \lambda \end{cases} $$

Method - Mahalanobis distance for OOD detection

An out-of-distribution (OOD) detection method which has gained a lot of research interest is measuing the distance of a test input to the training data in the network’s latent space. The distance metric used is typically Mahalanobis distance. Using a feature extractor $\mathcal{F}$ (which is typically a section of the DNN), the feature maps after a module in the network can be extracted $h(\mathbf{x}) \in \mathbb{R}^{D \times D \times M}$, where the maps have size $D \times D$ with $M$ channels. The means of these feature maps can be used to define an embedding vector $\mathbf{z}(\mathbf{x}) \in \mathbb{R}^{M} = \frac{1}{D^2} \sum_D \sum_D \mathbf{h} (\mathbf{x})$. The mean $\mathbf{\mu_y}$ and covariance matrix $\Sigma_y$ of the embedding vector for each class in the training data $(\mathbf{x},y) \sim \mathcal{D}_{\text {train}}$ can then be calculated.

The Mahalanobis distance $d_{\mathcal{M}_y}$ between the vector $\mathbf{z}(\mathbf{x}^*)$ of a test data point $\mathbf{x}^*$ and the training data of class $y$ can be calculated as a sum over $M$ dimensions.

$$ d_{\mathcal{M}_y}(\mathbf{x}^*) = \sum_{i=1}^M ( \mathbf{z}(\mathbf{x^*}) - \mathbf{\mu_y}) \Sigma_y^{-1} ( \mathbf{z}(\mathbf{x^*}) - \mathbf{\mu_y}) $$

The Mahalanobis score is defined as the minimum Mahalanobis distance between the test data point and the class centroids of the training data, which can be used as an OOD scoring function $\mathcal{S}$.

$$ \mathcal{S}_{\text {Mahal. Score}}(\mathbf{x}^*) = - \min_{y \in \mathcal{Y}} \{ d_{\mathcal{M}_y}(\mathbf{x}^*) \} $$

where the negative sign is used to stay consistent with the convention of having a higher scoring function for ID than OOD inputs.

Mahalanobis score is widely used for OOD detection, but its performance is mixed in the literature. It performs well in some studies but less well in others. So we wanted to study the best practises for this method. To study this method, we tested our models on Chest X-ray images from the CheXpert dataset.

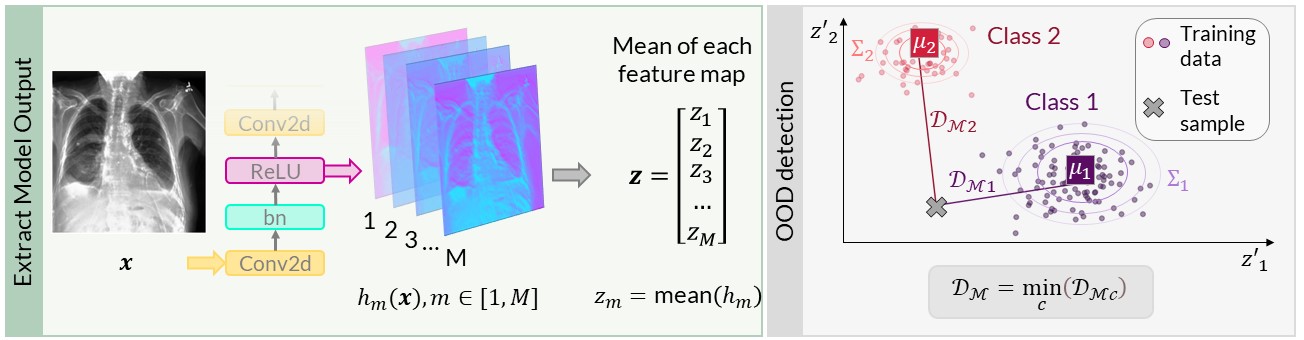
Figure 1: (Left) Method to extract embeddings after a network module. (Right) Mahalanobis score $d_{\mathcal{M}}$ of an input to the closest training class centroid. Figure is from [1].

New OOD detection evaluation dataset

We wanted to find validate our findings on a real-world OOD dataset. However, most OOD medical image tasks have irregular artefacts, which complicates analysis of OOD patterns. Therefore, we decided to create a clean and reliable OOD evaluation benchmark for medical imaging: we manually annotated approximately 50% of the frontal x-rays in the CheXpert dataset, creating a class of images with no support devices, that can be used as training data, and a class of images with pacemaker devices, which contain a visually distinct image pattern and can be used as the OOD test set. As a contribution of this work, we make these manual annotations publicly available, which can be accessed on my GitHub, and hope they will be useful for the community for assessing OOD methods on a real OOD artefact.

Key findings

Here are some of the key findings of our analysis:

Where you apply Mahalanobis score matters!
- Applying the method on the at final layer of a network is (very) suboptimal, despite being the most common application of this method!
- Applying the method after a ReLU operation generally improves the performance.
We also showed that different OOD patterns are optimally detectable at different depths of the network, there is no one single layer that can optimally detect all patterns.
We demonstrate that using multiple detectors at different depths of the network (for detecting different types of OOD patterns) can improve upon OOD detection.
This motivates future work on design and calibration of multi-detector systems for OOD.

Dive into our research!

📄 Paper

📊 Poster

</> Code